Turbo Vado 2 4.0 or 5.0 or 6.0?

[mcdenny]

Digging deeper into the rider power / motor power topic, using the Specialized support info linked in Allan's post above:

Since the motor produces a maximum of 300 watts at the pedal crankshaft at an 80 cadence,
20/100 means each rider watt is matched by (300/520) 0.58 motor watts
50/100. .............0.78 motor watts
60/100 ..............0.94 motor watts. motor power approximately equals rider power.
70/100...............1.12 motor watts
100/100..............3.53 motor watts. You + 3.5!

 

[Jeremy McCreary]

Thanks Jeremy. I'm an engineer too and appreciate your very detailed posts on how the specialized motor controller works.

My curiosity has to do with this: Lets say I'm riding in ECO (20/20) at maybe 12 mph at saturation. If I want to go faster it's all me. But if ECO is 20/100 all else being equal, if I want to go faster the motor will still be helping me (You, only faster, right). m Is my understanding correct?

Correct. Below saturation, motor power Pm depends on assist mode E/M only via E, and above saturation, only via M.

Since E = M = 20 in the 20/20 case, you'd necessarily saturate at rider power Pr = P1 = 139W. Motor power would be

Pm = B Pr (E / 100) = 64W,

where boost B = 2.3 for your motor. Total power at the crank would then be Pc = Pr + Pm = 203W, which buys ground speed Vg = 12 mph in this example.

At assist 20/100, Pm would still be 64W at Pr = P1 since E = 20 hadn't changed. But saturation's now pushed out to Prs = P1 (M / E) = 695W. So pushing Pr above P1 would definitely get you more Pm, Pc, and Vg.

For example, at Pr = P1 + 100W = 239W, you'd still be far below Prs. Then Pm = 110W and Pc = 249W, which would definitely get you above 12 mph under the same conditions.

 

[Jeremy McCreary]

Digging deeper into the rider power / motor power topic, using the Specialized support info linked in Allan's post above:


View attachment 205046

Since the motor produces a maximum of 300 watts at the pedal crankshaft at an 80 cadence,
20/100 means each rider watt is matched by (300/520) 0.58 motor watts
50/100. .............0.78 motor watts
60/100 ..............0.94 motor watts. motor power approximately equals rider power.
70/100...............1.12 motor watts
100/100..............3.53 motor watts. You + 3.5!

I like this way of looking at it!

 

[Stefan Mikes]

My curiosity has to do with this: Lets say I'm riding in ECO (20/20) at maybe 12 mph at saturation. If I want to go faster it's all me. But if ECO is 20/100 all else being equal, if I want to go faster the motor will still be helping me (You, only faster, right). Is my understanding correct?

According to Specialized, you need 117 W to saturate the SL 1.2 motor at 20/20%. (The Ease 20% means the Assist of 0.54x). If you input 117 W of leg power or more, the motor would provide a steady assistance of 64 W. Whatever extra you can input is just you.

Again, Specialized says you need as much as 553 W to saturate the SL 1.2 motor at 20/100%, that is, you need to input that much power to produce 320 W mechanical from the motor. Whatever leg power you input up to 553 W will result in a motor response, so yes, you will ride faster and faster.

@Jeremy McCreary, I cannot get any consistent information about the SL 1.2 actual Boost Factor. Are these data consistent in your opinion? The max motor power is 320 W.

• According to this table, Pr = P1 = 117 W not 139 W at 20/20%
• Is the Boost Factor = 3.2 based on these tables?

 

[Jeremy McCreary]

@Jeremy McCreary, I cannot get any consistent information about the SL 1.2 actual Boost Factor. Are these data consistent in your opinion? The max motor power is 320 W.

Those tables are NOT consistent with my simple, steady-state model of the Specialized power-sensing assist. Will have to delve into that.

Based my model and the boost B = 2.3 for the 1.2 SL motor on official Specialized documention put out prior to the SL 2, when the Creo 2 was the only bike using that motor. I linked the official motor summary showing B = 2.3 for you previously. Will see if I can find the link again.

That documentation gave a max mechanical power Px = 320W and boost B = 2.3. It also talked of linear relationships between E and B and Pm (motor power) below saturation and between M and Px and Pm above saturation.

That linearity implied a saturation rider power Prs of

Prs = (Px / B) (M / E) = P1 ( M / E),

where Px, B, and P1 = Px / B are all motor constants supposedly independent of E and M.

So, when E = M, both M and E cancel out of Prs, leaving Prs = P1, a constant. Based on Px = 320W, and B = 2.3, P1 = 139W.

But your upper MicroTune table — which wasn't available then — shows that Prs is clearly NOT constant when E = M. So there must be previously unmentioned nonlinearities in the system. Not entirely surprising in retrospect but not anticipated from earlier documents.

It's also possible that the SL 2 uses a modified version of the earlier 1.2 SL motor.

 

[mcdenny]

one more little wrinkle, a bit higher up in that support document there is a graph of motor mechanical power output vs pedal RPM. 320 w is the max at 90 RPM. It drops to 300 w at 80 RPM.

 

[mcdenny]

Further combining the two tables and assuming the motor torque multiplier is linear for a given "ease" setting this shows the total, rider and motor power vs ease when pedaling at saturation with E=M.

 

[Jeremy McCreary]

one more little wrinkle, a bit higher up in that support document there is a graph of motor mechanical power output vs pedal RPM. 320 w is the max at 90 RPM. It drops to 300 w at 80 RPM.

Wish they'd publish detailed info like that for my SL 1.

Below is a graph comparing the official SL 2 tables of Prs values for regular and dynamic MicroTune modes to the predictions of my simple linear model. E is on the horizontal axis, and Prs on the vertical.

Revised the linear model to use the official max power of Px = 300W for the 80 rpm cadence used in the official tables. But stuck with boost B = 2.3 here, as the B = 3.2 suggested by @Stefan Mikes made the linear predictions even worse.

For the regular MicroTune case with E = M, the linear model predicts a flat Prs = P1 = 130W independent of E (yellow line). But the official table indicates a convex upward curve (blue) with significant variation in Prs as a function of E.

For the dynamic MicroTune case with variable E but fixed M = 100, the linear model predicts a hyperbolic Prs curve (green line). But the official table indicates a nearly linear decline in Prs with E (blue).

Having no reason to doubt the official SL 2 data, gotta conclude that the linear relationships between E, M, and motor power described in earlier Specialized documents aren't really linear in the SL 2.

Will look into this further. In the meantime, disregard my posts 19 and 22 above.

 

[mcdenny]

Final chart, I promise. This shows total power for each dynamic (power not capped) micro tune setting with the rider providing 100 watts in every case. This is probably a more meaningful analysis. I for one could manage a steady 100 watts but not for a very long time. When I get my new bike and the weather cooperates I'll find a level place to try to gather some real world data

Jeremy, do you have a formula to estimate how fast 170# me would go at 450 watts?

Quite small differences in the lower settings but big increases at steps 7-10. It would be interesting to put a bike on a stationary trainer that would output total watts at the rear wheel and get some actual data.

PS: Here's the view out my kitchen window in Nashville right now. It's the reason I'm doing Excel spreadsheets instead of riding my bike. I'd rather be riding.

 

[Stefan Mikes]

as the B = 3.2 suggested by @Stefan Mikes made the linear predictions even worse.

A typo, sorry. Should be 2.3.

 

[Stefan Mikes]

Guys, let me tell you what.

Vado SL 1 can climb 10% inclines with mountain gearing and my very weak legs*. Vado SL 2 is 1/3 stronger. Why we even go into such details?
---------
*) Jeremy says he can climb even more serious inclines.

 

[Jeremy McCreary]

Guys, let me tell you what.

Vado SL 1 can climb 10% inclines with mountain gearing and my very weak legs*. Vado SL 2 is 1/3 stronger. Why we even go into such details?

Why? Because I find it an interesting lens on riding my SL. If it doesn't interest you, please feel free to ignore.

 

[Jeremy McCreary]

Final chart, I promise. This shows total power for each dynamic (power not capped) micro tune setting with the rider providing 100 watts in every case. This is probably a more meaningful analysis. I for one could manage a steady 100 watts but not for a very long time.

Need to digest this graph. How did you get motor power?

When I get my new bike and the weather cooperates I'll find a level place to try to gather some real world data

Excellent! I'll try, too.

Jeremy, do you have a formula to estimate how fast 170# me would go at 450 watts?

No simple formula, but I have a spreadsheet that correlates well with my favorite online calculator by Steve Gribble.

To get ground speed Vg from rear wheel power, you have to solve a cubic equation in Vg. Luckily, there's a cubic formula analagous to the quadratic formula, but it really takes a spreadsheet to apply.

Is that 450W at the real wheel on your new SL 2? I'd need estimates of your drag area (CdA) and coefficient of rolling resistance (Crr). There are ways to estimate these key parameters, but not with great confidence. Your weight and the official SL 2 specs cover the rest of the necessary inputs.

View attachment 205082

Quite small differences in the lower settings but big increases at steps 7-10. It would be interesting to put a bike on a stationary trainer that would output total watts at the rear wheel and get some actual data.

Yes, we really need some solid data to understand how our power-sensing PAS really works. Those MicroTune tables from Specialized are a start.

 

[mcdenny]

Guys, let me tell you what.

Vado SL 1 can climb 10% inclines with mountain gearing and my very weak legs*. Vado SL 2 is 1/3 stronger. Why we even go into such details?
---------
*) Jeremy says he can climb even more serious inclines.

Because its fun to know how stuff works!

 

[mcdenny]

Need to digest this graph. How did you get motor power?
The dynamic micro-tune table gives rider power to get full motor power. We know max motor power at 80 cadence = 300 watts. 300/rider power to get max motor power= motor watts per rider watt. e.g. 30/100 required 503 rider watts so 300/503 =0.596. If rider is producing 100 watts motor will give 59.6 watts with 30/100 setting. I really don't know if each "ease" setting is setting the slope of the rider power/ motor power curve or if it is linear at all.


Excellent! I'll try, too.


No simple formula, but I have a spreadsheet that correlates well with my favorite online calculator by Steve Gribble.

To get ground speed Vg from rear wheel power, you have to solve a cubic equation in Vg. Luckily, there's a cubic formula analagous to the quadratic formula, but it really takes a spreadsheet to apply.

Is that 450W at the real wheel on your new SL 2?

It should be 400 watts at the rear wheel. The tables suggest at 100/100 85 rider watts gets you 300 motor watts so 100 rider + 300 motor = 400 total. The 450 watts at 100/100 on the graph above is a mistake. At 100/100 motor watts = rider watts * 3.53 up to a max of 300 watts. My mistake was to not cap motor power at 300 in my spreadsheet. Mea culpa.

I'd need estimates of your drag area (CdA) and coefficient of rolling resistance (Crr). There are ways to estimate these key parameters, but not with great confidence. Your weight and the official SL 2 specs cover the rest of the necessary inputs.

Google AI says my drag coefficient = 0.6 and frontal area = 5.4 ft2. The formula says my top speed will be 27 mph. Gee, pretty close to the 28 mph class 3 limit. Interestingly, it says just the 100 rider watts should give 16 mph. That seems high to me. You?

Yes, we really need some solid data to understand how our power-sensing PAS really works. Those MicroTune tables from Specialized are a start.

 

[Jeremy McCreary]

At 100/100 motor watts = rider watts * 3.53 up to a max of 300 watts.

OK, I see what you're doing here. Clever use of the dynamic MicroTune table!

For each E, you can extract the slope S(E) of the chord of the Pm vs. Pr curve between (0,0) and the saturation point (Prs,Px), where Px = 300W for the SL 2 at 80 rpm. These slopes increase nonlinearly with E.

Even if the curve's not truly linear before saturation, this is still a more empirical way to calculate Pm from Pr than what I've been doing. You've given me an idea...

Google AI says my drag coefficient = 0.6 and frontal area = 5.4 ft2. The formula says my top speed will be 27 mph. Gee, pretty close to the 28 mph class 3 limit.

Assuming a 170 lb you on a bare SL 2 5.0 on flat, smooth pavement in still air, my speed-from-power spreadsheet also gives 27 mph from 400W at the rear wheel.

Those frontal area and Cd figures give CdA = 0.3 m², which is getting into road racer territory. The power Pa lost to air resistance totally dominates total power loss at 27 mph on the flat. This Pa is proportional to CdA, so CdA matters.

Pa swamps any effect of Crr in this scenario, but I estimated your bike's Crr by arbitrarily adding 5% to the 0.00689 Crr measured by www.bicyclerollingresistance.com for my 38 mm tubeless Pathfinder Pro gravel tires.

Interestingly, it says just the 100 rider watts should give 16 mph. That seems high to me. You?

I get 15 mph. And it does seem high but not preposterous. Next ride, I'll see how fast my SL 1 goes on the flat in OFF at Pr = 100W.

 

[Stefan Mikes]

Why? Because I find it an interesting lens on riding my SL. If it doesn't interest you, please feel free to ignore.

Because its fun to know how stuff works!

I apologise for the miscomprehension. As you two should know, I'm very interested in the operation of Specialized ebikes, only the latest information looks strange to me.

We knew, and could experimentally prove, the following facts about the SL 1.1 motor:
Max Assist (Boost): 1.8x
Max Mechanical Motor Power: 240 W
Max Electrical Motor Power: 303 W
Max Motor Torque: Rated 35 Nm @ 60 rpm (reference rotational speed as the motor spindle). That is: 240 W / 6.28 rad/s = 38.2 Nm.

The marketing data for the SL1.2 motor were:
Max Assist (Boost): 2.3x (2.3 / 1.8 = 1.27 x)
Max Mechanical Motor Power: 320 W (320 / 240 = 1.33 x). If we, however, use the 300 W maximum power figure, it is 300 / 240 = 1.25, which is similar to the ratio of Max Assist for both motors.
Max Electrical Motor Power: n/a
Max Motor Torque: Rated 50 Nm. If we use the standard 60 rpm reference, the calculated torque would be 320 / 6.28 = 51 Nm or 300 / 6.28 = 47.8 Nm.

Now, we learn it is 320 W at the cadence of 95 rpm or 300 at 80 rpm. Stranger and stranger. On the other hand, the torque chart shows the maximum at a very low cadence!

The last straw is this data row of the table: 100/100%. The rider would saturate the motor at 85 W leg output. So the Max Assist Factor (Boost) would either be 300/85 = 3.53 or even 320/85 = 3.76. It is nowhere close to the B = 2.3! Such high Boost Factor is for Full Power Specialized motors!
----------------
Something is really sus there. Such inconsistent data are well above my pay grade. Also, there is something such as an experiment.

With Gen 1 TCU 1, we could get experimental data using BLEvo app. That's why I said the data for SL 1.1 could be experimentally verified. As I can understand, either the Mastermind TCU or the H3 display as well as the Specialized App can produce these data:

• Rider Power
• Motor Power (Electrical?)
• Rider Power / Motor Power (or, the reciprocal)

When @mcdenny gets his Vado SL 2 with H3, he can set off for a ride in the ideal cycling conditions and just watch the measured data himself. That would be a very very interesting experiment.

Thank you both for the patience.

P.S. Once, there was a Specialized Support page called "Motors", which listed the rated parameters of each and every Specialized motor. That page seems to have disappeared. I wonder why.

 

[Jeremy McCreary]

Buckle up, Specialized nerds!
Went back to my linear model based on official pre-SL documentation. Here are 3 screen shots of the interactive graphical version at

Specialized mid-drive power-sensing PAS

www.desmos.com

Here's the setup. Px = 300W is the SL's max mechanical motor power at 80 rpm cadence. B = 2.3 is the boost factor originally published for the SL 2's motor.

We're writing a Spec assist mode like my ECO (35/45) as E/M. As a motor property, B should be a constant, independent of both E and M.

This model's "linear" in that motor power Pm is directly proportional to E, B, and rider power Pr below saturation and proportional to both Px and M but independent of Pr above saturation. As indicated in pre-SL 2 documentation.

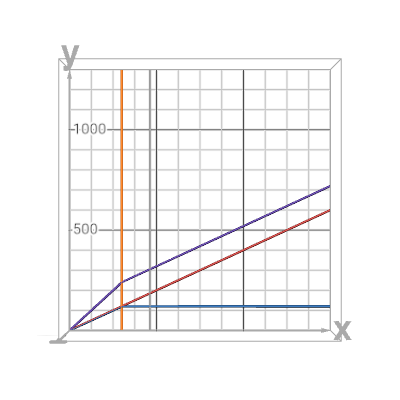
Here's a closer look at the model graph for E = M = 50. Pr plots on the horizontal axis and various kinds of power at the crank plot on the vertical axis.

Let's focus on the blue Pm plot and its pre-saturation ramp and post-saturation flat. Any realistic model of Specialized's power-sensing mid-drive PAS must capture the following features:

o Since Specialized mid-drives have no throttles, the Pm ramp must start at (0,0). Check.

o Since post-saturation Pm is fixed at the cap imposed my M, the post-saturation Pm plot must be a horizontal straight line. Check.

o Since I never feel a thing when I pedal my SL 1 through Prs, the ramp and flat must meet at Prs. No jumps. Check.

o The orange vertical automatically marks the Prs (saturation Pr) predicted by the model. It always falls at the ramp-flat intersection, just as it should. Check.

Discrepancies
In the E = M = 50 case, the model predicts Prs = 130W, as shown by the orange vertical above.

But something's wrong, cuz the Specialized Prs table for the SL 2's regular MicroTune gives Prs = 200W for E = M = 50 at 80 rpm. I used the graph's Pri slider to mark this official value with a gray vertical. Big discrepancy.

Now let's look at the model graph for the E = 50, M = 100 case:

Model says Prs = 261W (orange vertical), but the official Prs table for dynamic MicroTune says Prs = 385W (gray vertical). Even bigger discrepancy.

NB: To clean up the math ahead, we'll set E' = E / 100, and M' = M / 100. This makes E' and M' numbers between 0 and 1, inclusive.

How to fix the model?
So what's left to tweak to bring this model into agreement with the official SL 2 MicroTune tables above? If we keep the seemingly safe model assumption that the saturation motor power Pms = Px M', the only wiggle room left is in the shape or slope of the pre-saturation Pm ramp.

Can we win there somehow? Maybe.

Fix the ramp's shape?
You'll be relieved to know that we don't have the data needed to correct ramp shape by switching to a nonlinear relationship between Pm and Pr. Dead end.

Just fix the ramp's slope?
But we do have the data for a stab at a slope fix. If we keep the Pm ramp a straight line — i.e., keep Pm there strictly proportional to Pr — how could we fudge the slope to get official SL 2 Prs values out of the linear model?

In the existing model, the linear Pm ramp is given by

Pm = E' B Pr,

with slope S = E' B. Boost B is supposedly a motor constant baked into the SL 2, so no fudging opportunities there. Simply picking a different constant B value won't get the job done.

The only way forward would be to introduce a fudge factor F that's a nonlinear function of E, like so:

Pm = F(E) E' B Pr,

so the ramp slope becomes S = F(E) E' B

For the dynamic MicroTune table, this fudge factor F would vary with E as shown in the last column below:

EDIT: F values (column D) corrected Jan 27, 2026.

Since E only comes in multiples of 5, it'd be easy enough to interpolate the above into a complete E-based look-up table for code or spreadsheet use. A Desmos graphical model might also be possible.

But what about the regular (E = M) MicroTune Prs data? This F(E) fudge factor has at least the right shape to work there, too. Stay tuned.

EDIT Jan 27, 2026: The F values above correct the Prs model for M = 100, but DO NOT correct the Prs model for E = M.

 

[Stefan Mikes]

I just think the data for the last data row is wrong (Specialized fault). It looks good for other data rows.

 

[Rás Cnoic]

This whole thread is making my head hurt. I haven't a notion what all the maths means here, haven't the brain for it, start seeing blurry! Don't stop yer workings, it's fascinating in a remote detached way.

All I know is I can get up any 20% even 25% gradient on my 5 year old Vado SL with 36/11-46. Once you have low enough gears & a bit of patience and a good line, that puny 35nm motor gets the job done. Would love to try the Creo 2 and feel the difference. Or compare to TQ40 & 60. So many good options these days.