Crossover speeds

[Jeremy McCreary]

My mind wonders when I ride. And when I'm really feeling the total resistance (TR), it sometimes wonders which part I'm fighting most at that moment — air resistance (AR), slope resistance (SR), or rolling resistance (RR)?

Since the question's not entirely academic, decided to find out with a little help from Google Sheets and my bike engineering bible, Bicycling Science (Wilson and Schmidt, 2020, 4th ed). Started close to home with an upright 200 lb rider in street clothing on a 65 lb commuterish ebike on smooth pavement at ground speeds up to 12.5 m/s (28 mph).

Below are some of the resulting plots. These let me find the "crossover" ground speed (Vc) at which AR becomes 50% of TR for the bike and rider above. As ground speed (Vg) leaves Vc behind, AR's piece of the TR pie can only grow, and quickly. Having some feel for which side of Vc you're on could come in handy when you need to conserve battery or legs.

Looked at 4 common cases:
A. No wind, no grade
B. No wind, 5% grade
C. Moderate (4.5 m/s, 10 mph) headwind, no grade
D. 4.5 m/s headwind, 5% grade

Each plot splits out the relative contributions that AR, SR, and RR make to TR. They show power loss rather than resistance, but the relationships are exactly the same through either lens. Note that these plots say nothing about TR itself. I try to give some idea of how TR varies from case to case in the text. Look for Vc in each case.

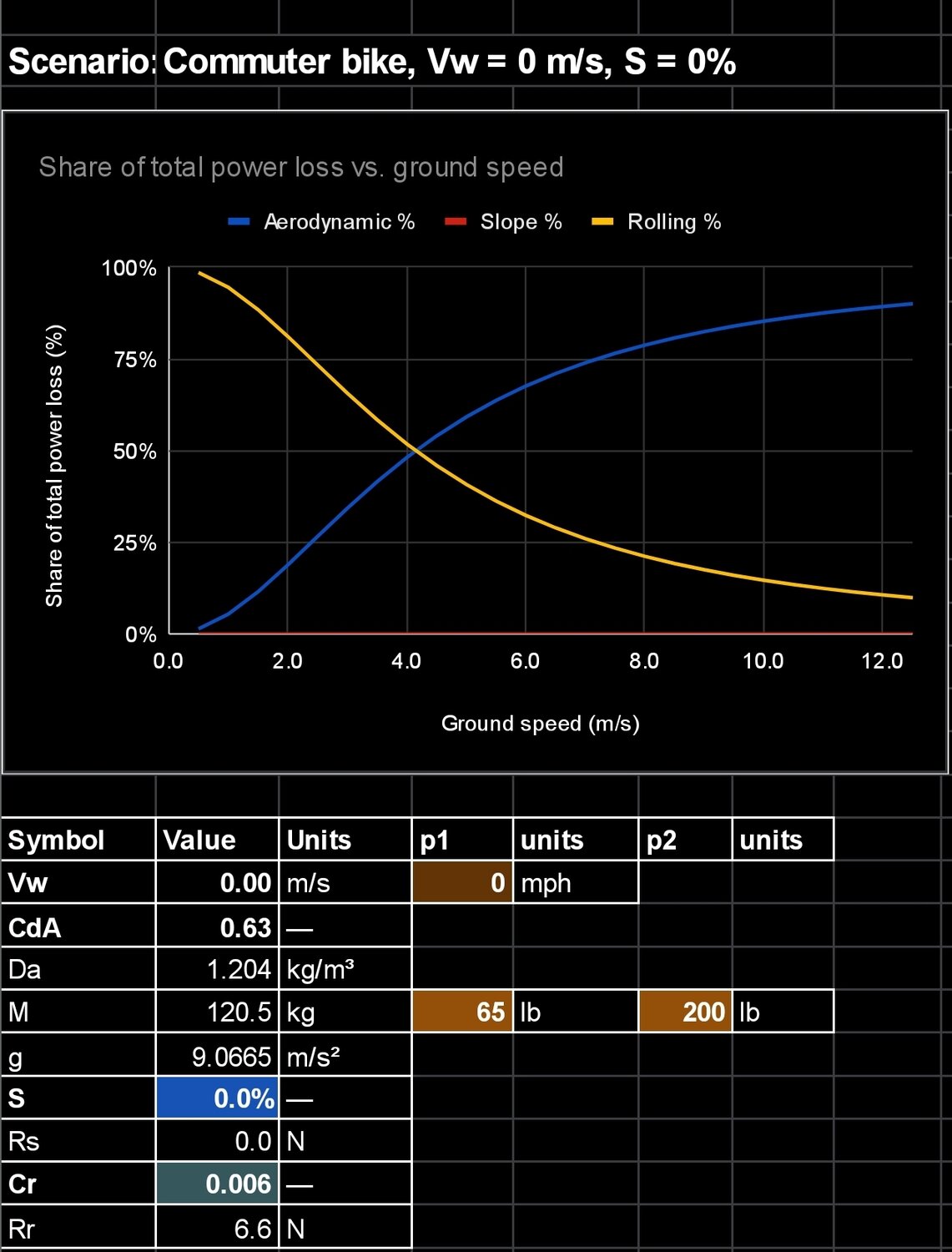
Case A: No wind, no grade, Vc ≈ 4.1 m/s (9 mph). Compared to the other cases, TR is at a minimum at all speeds, and below this rather slow Vc, RR dominates.

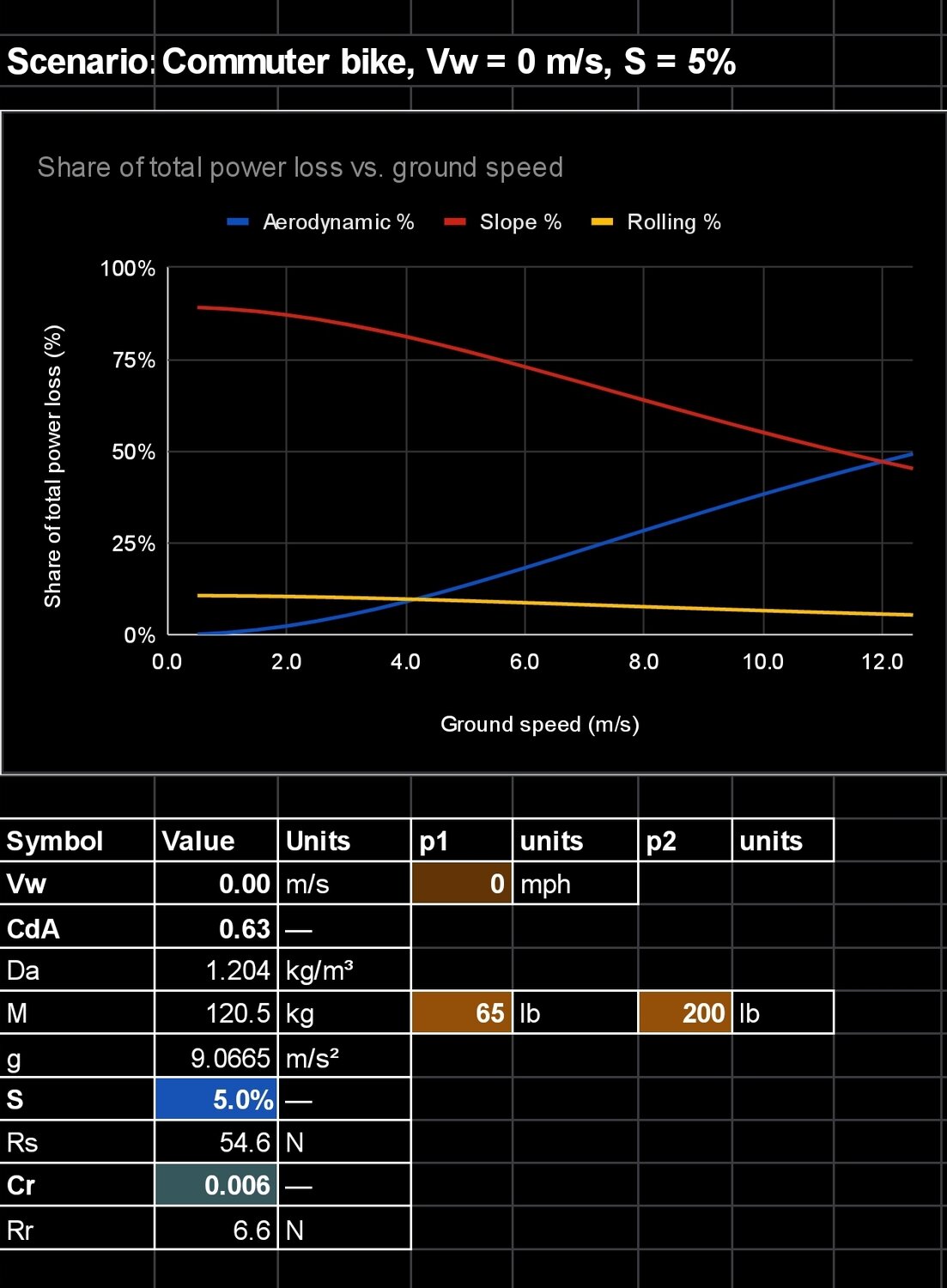
Case B: No wind, 5% grade, Vc ≈ 12.5 m/s (28 mph). TR is significantly greater than in Case A at all ground speeds, and below Vc, SR dominates.

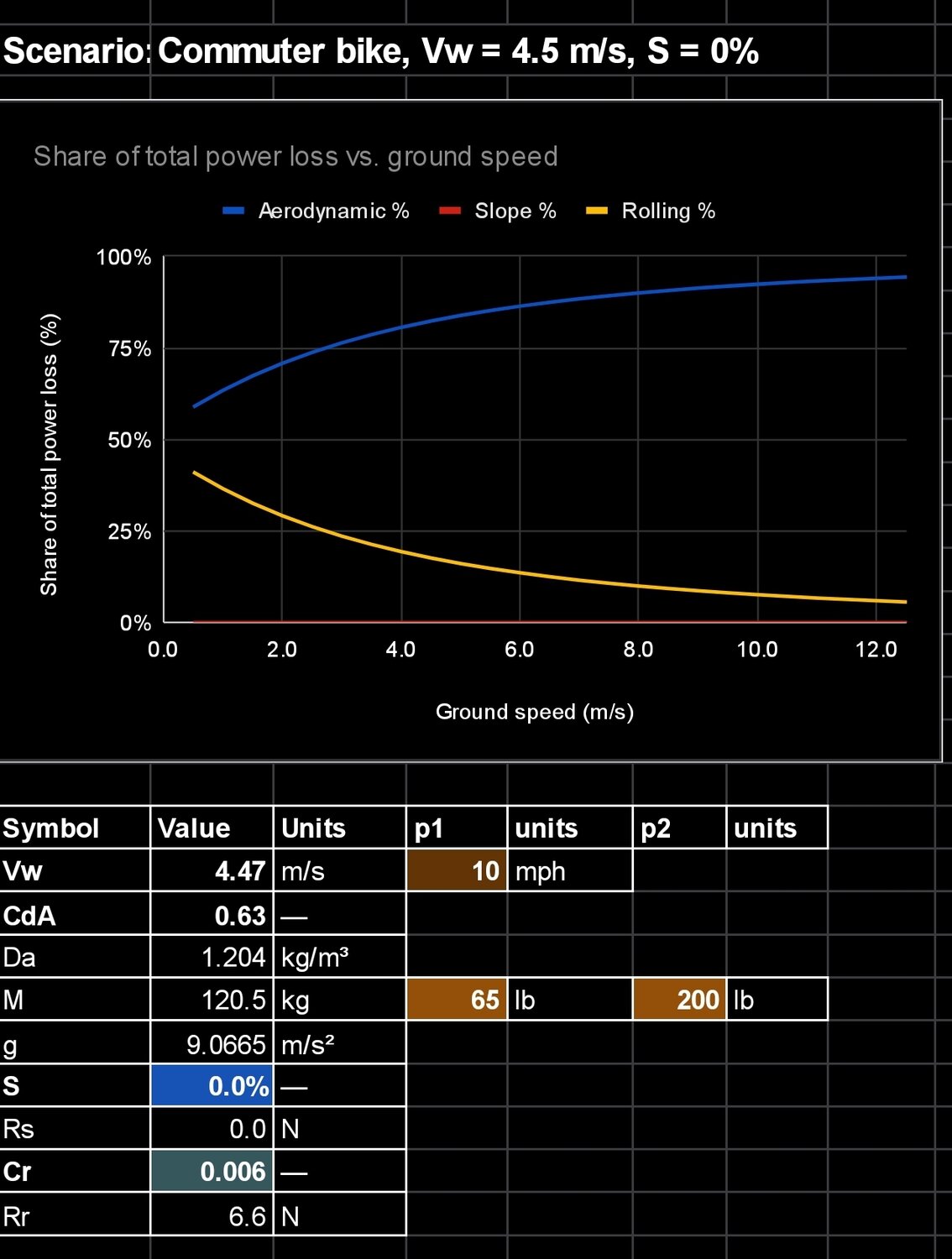
Case C: Moderate (4.5 m/s, 10 mph) headwind, no grade, Vc ≈ 0 m/s (0 mph). TR is less than in Case B at all ground speeds, and AR dominates throughout.

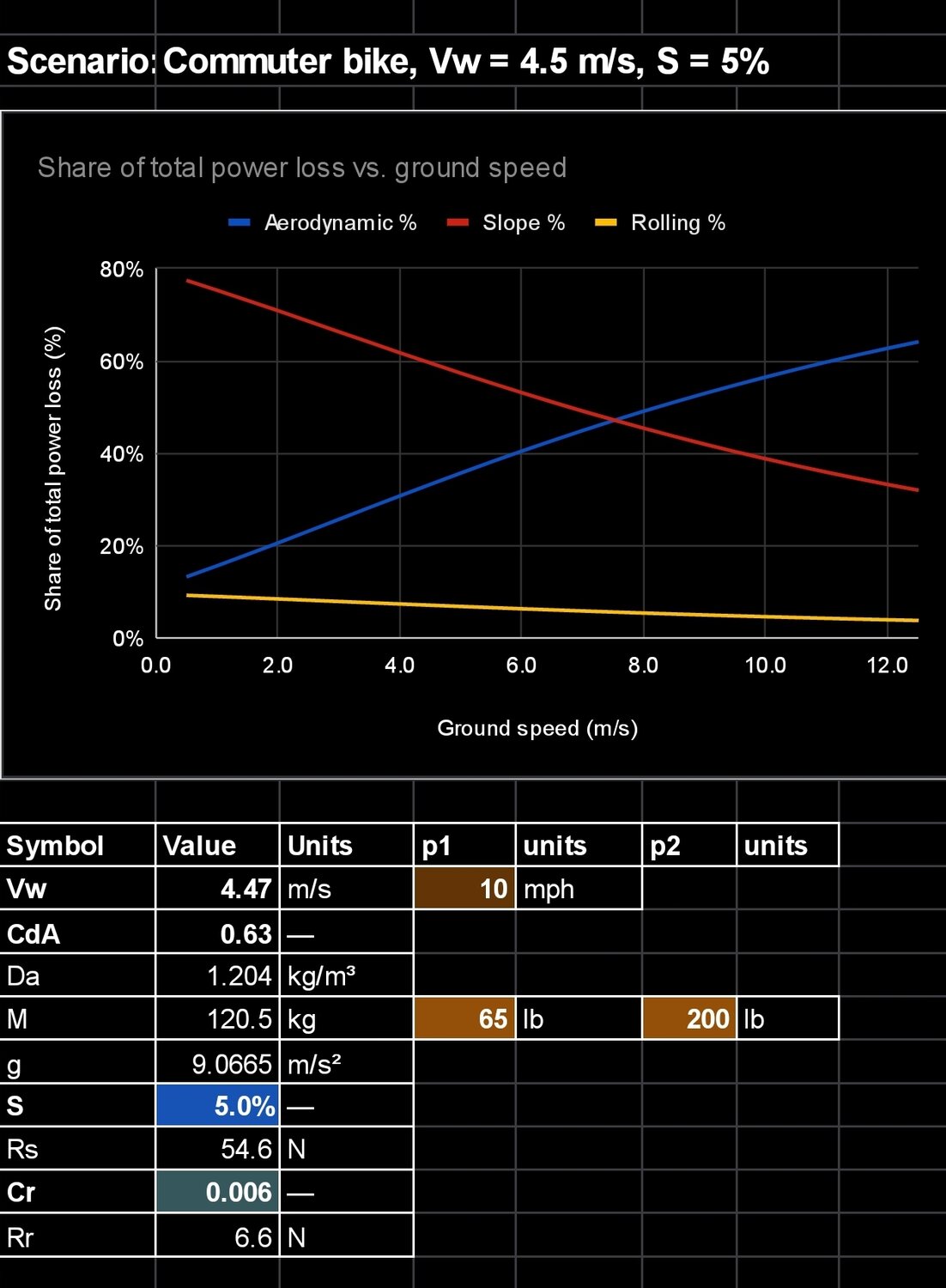
Case D: 4.5 m/s headwind, 5% grade, Vc ≈ 8.0 m/s (18 mph). Compared to the other cases, TR is maximal at all ground speeds — even below Vc, where SR dominates.

Things to note
AR and RR are always present, and AR always dominates TR sooner or later — until even a moderate hill intervenes. At that point, you may get nowhere close to Vc. Not much point in tucking then.

AR grows with the square of airspeed — which of course exceeds Vg in a headwind — but is unaffected by total (bike+rider) weight. Conversely, SR and RR grow linearly with total weight but don't change with speed. RR dominates TR only at very low Vg on the flat with no wind.

A closer look at the plots
Case A vs. B: With no wind and no grade (A), Vc ≈ 4.1 m/s but jumps to 12.5 m/s when a 5% grade comes along (B). Since the latter Vc is generally out of reach on a 5% uphill, SR dominates TR at all feasible speeds in Case B.

Case C vs. D: In a 4.5 m/s headwind, Vc drops to zero on the flat (C) but jumps to 8.0 m/s on adding a 5% grade (D). Since AR will be your main nemesis at all speeds in Case C, makes sense to reduce it on long, flattish rides into a headwind at low or no assist. Your battery and legs will thank you.

Case B vs. D: On a 5% grade, Vc ≈ 12.5 m/s in still air (B) but drops to 8.0 m/s when the headwind comes up (D). Since you're unlikely to reach Vc in either case at low or no assist, small AR countermeasures make little sense.

As you can guess from these trends, reducing AR by getting the rider to streamline by wearing lycra and tucking will raise all Vc values and reduce all TRs. When your goal is to ride far and fast with little or no assist, this can be a signicant effect. The roadies know what they're doing in this regard.

Explanation of symbols in tables accompanying plots (all in SI units)
o Vw = wind speed component in direction of travel relative to ground, headwind-positive
o CdA = drag area
o Da = air density at sea level
o M = mass of bike+rider system
o g = standard acceleration of gravity
o S = road gradient
o Rs = slope resistance
o Cr = coefficient of rolling resistance
o Rr = rolling resistance

Source
The necessary bike and rider parameters CdA and Cr came from Table 5.1, p. 230, Wilson and Schmidt, 2020, Bicycling Science, 4th ed. All resistance and power loss formulas came from elsewhere in the same book, as did determinations of the losses safely ignorable here.

 

[AHicks]

Pretty impressive thoughts going on here! "My mind wonders when I ride."

My focus would likely have been on the weather or how comfortable I was at the moment!!!

 

[Jeremy McCreary]

Pretty impressive thoughts going on here! "My mind wonders when I ride."

My focus would likely have been on the weather or how comfortable I was at the moment!!!

You know you're a hopeless nerd when Physics Today is your favorite magazine. Put that guy on a bike, and this is what happens. However, I mostly think about more normal things — like how nice it is to be outside, how lucky I am to be riding again, and how much my butt hurts.

Riding neighborhood laps at zero assist with my next-door neighbor really brought resistances into focus. When we both stop pedaling on the same 3% downhill at 10 mph, he and his fancy sub-20 lb Italian road bike out-coast me every time. And this despite the extra gravity assist I get by carrying at least 40 more lbs in bike weight alone.

Probably a combo of reduced air and rolling resistance on his part. I'm upright in street clothes on 2.3" hybrid tires at 40-50 psi. He's semi-tucked in tighter clothing with slick skinny road tires at twice the pressure. My tires are the only ones you can hear.

At 10 mph, I'm close to my own flat windless crossover as we start to descend, but he's probably below his. He no doubt has better wheel bearings, but my source says that bearing resistance is negligible in non-racing contexts.

 

[Jeremy McCreary]

Best discussion of cycling power requirements I've seen, from Grin Technologies...

 

[PCeBiker]

My mind wonders when I ride.

Me too.

AR grows with the square of airspeed — which of course exceeds Vg in a headwind

He said in the video that wind resistance grows with the cube of the airspeed, and that seems closer to what I've observed on my e-bike.

I am obsessively checking my Watt meter when I ride and try to keep my motor power under about 300 Watts.

I slow down in a headwind, and speed up with a tailwind to try to get a consistent motor power output.
(And as you know I contribute nothing, unless I have to. )

 

[Jeremy McCreary]

He said in the video that wind resistance grows with the cube of the airspeed, and that seems closer to what I've observed on my e-bike.

Yes, he did. But he was talking about the power lost to air resistance, and I was talking about the resistance itself. A resistance is a net force directly opposing forward motion. Resistance is measured in Newtons, power in Watts. Two very different physical quantities.

In cycling, the power P lost to any resistance R at groundspeed Vg is

P = R Vg.

In still air, the air resistance at speed Vg is

Ra = Ka Vg²,

where Ka is a constant depending on air density, rider position and clothing, and other size-and-shape factors pretty much fixed on a given ride. So the power lost to Ra in still air is

Pa = Ra Vg = Ka Vg³

It's really important to distinguish to between power and resistance.

 

[PedalUma]

From Sheldon Brown:

 

[PCeBiker]

Yes, he did. But he was talking about the power lost to air resistance, and I was talking about the resistance itself.

Pa = Ra Vg = Ka Vg³
It's really important to distinguish to between power and resistance.

OK I think that I got my head wrapped around that now.
(I haven't done any real math or physics since 1983. )


My biggest take away is the cubed relationship between speed and the power required to push through the created wind.

If I increase my speed from say, 15 mph to 45 mph, it takes 27 times more Watts/power to push through it. Not 3 or 9 times as much.

PAS sensing e-bikes (all e-bikes except mine. ) kinda give you a false sense of how much power your e-bike is using. Especially simple cadence sensing e-bikes where you can ghost pedal.

Knowing how many Watts your e-bike is using at any given time, can go a Long way towards guesstimating battery life and range.

Things like road resistance and hill climbing are more consistent than wind.
Wind can be up and down all day long, and maybe changing direction during the ride.
Planning a ride based on wind can get really tricky, especially when it is a cubed relationship between wind speed and the power needed to overcome it.

 

[PCeBiker]

My mind wonders when I ride.

My mind tends to wander more than wonder.
I'm prone to getting lost.

 

[PedalUma]

27 times more Watts

A guy with a new 6-week bike took a Summer's afternoon ride from his town to mine. On his driveway the duel battery setup showed a range of 222 miles. It died as it came into my town 12-15 miles away because of the 32 mile per hour headwinds. I had to take it all the way down with the USB and fully recharge it to balance load. Then sent him for warranty service. He had run it all the way down and left it parked there four times after using the throttle. It was a $6500 bike from New Wheel in Larkspur, CA. Heavy as sin.

 

[Jeremy McCreary]

PAS sensing e-bikes (all e-bikes except mine. ) kinda give you a false sense of how much power your e-bike is using. Especially simple cadence sensing e-bikes where you can ghost pedal.

Knowing how many Watts your e-bike is using at any given time, can go a Long way towards guesstimating battery life and range.

My display has a nice motor power graphic, but I'd rather see a number in Watts like you have. Would also love to see a number on the Watts I'm putting into the pedals — mainly just out of curiosity. Not willing to spend the money on my current ebike, but next time...

 

[PCeBiker]

My display has a nice motor power graphic, but I'd rather see a number in Watts like you have.

My Watt meter kinda sucks. It's weighted or averaged or doing a stupid logarithm or something.
If I kill the motor from full power, it takes about 10 seconds for it to drop and read 0.
If it gets full power it takes about 5 seconds to read maximum.
It's too slow and I can't see the power spikes.

I just decided to get one of these,..
Ten bucks,..

I got the 20 amp version because I have my 25 amp controller turned down to half.
I got the 75 mV meter that needs the shunt because I didn't want the full 20 amps running up to my handlebars and into a 3 dollar meter.
Now the meter can crap out, but it won't kill my ebike.

I've already got this to install, but I prefer pointers.

Would also love to see a number on the Watts I'm putting into the pedals — mainly just out of curiosity.

I managed to get a bit of reading by riding along on level pavement with a steady breeze and my throttle locked, then I started pedaling for about 10 seconds.
The power output dropped by about 125 Watts.
That was a pretty rough measurement though.

Not willing to spend the money on my current ebike, but next time...

One of these will give you all the information you need to do a lot of different calculations.
$60 CAD

 

[Art Deco]

OK I think that I got my head wrapped around that now.
(I haven't done any real math or physics since 1983. )


My biggest take away is the cubed relationship between speed and the power required to push through the created wind.

If I increase my speed from say, 15 mph to 45 mph, it takes 27 times more Watts/power to push through it. Not 3 or 9 times as much.

PAS sensing e-bikes (all e-bikes except mine. ) kinda give you a false sense of how much power your e-bike is using. Especially simple cadence sensing e-bikes where you can ghost pedal.

Knowing how many Watts your e-bike is using at any given time, can go a Long way towards guesstimating battery life and range.

Things like road resistance and hill climbing are more consistent than wind.
Wind can be up and down all day long, and maybe changing direction during the ride.
Planning a ride based on wind can get really tricky, especially when it is a cubed relationship between wind speed and the power needed to overcome it.

And you can see a hillclimb coming up, judge how high it is and turn back, etc. Can't see the wind and it may not stop for hours.

 

[PCeBiker]

And you can see a hillclimb coming up, judge how high it is and turn back, etc.

The area all around my place is almost perfectly flat, but I did get out in the dirt to do some hill climbing.
I didn't know what a "percent grade" was until I Googled it.
(I thought 100% grade would be straight up. I'm used to angles in math class.)

I turned my controller up to maximum (25 amps), put it in first gear, and got a running start towards a dirt hill full of rocks and deep ruts (made by quads).

The hill was pushing 100% grade (45°). It was at least a 35° angle and a 50 foot climb.

I looked down at my Watt meter a couple times and it was reading over 1200 Watts.

I just powered up the hill pedaling in first gear without stalling.
It kinda felt like the bike took itself up the hill and I pedaled myself up the hill.
There was no loss of momentum and I could manage a half decent cadence.

Remember, I've got an ebike that weighs almost 100 pounds with street tires, no rear suspension, 75 mm travel front forks, two mirrors, and a windshield.

Anything is possible.
You just have to try.

 

[Art Deco]

The area all around my place is almost perfectly flat, but I did get out in the dirt to do some hill climbing.
I didn't know what a "percent grade" was until I Googled it.
(I thought 100% grade would be straight up. I'm used to angles in math class.)

I turned my controller up to maximum (25 amps), put it in first gear, and got a running start towards a dirt hill full of rocks and deep ruts (made by quads).

The hill was pushing 100% grade (45°). It was at least a 35° angle and a 50 foot climb.

I looked down at my Watt meter a couple times and it was reading over 1200 Watts.

I just powered up the hill pedaling in first gear without stalling.
It kinda felt like the bike took itself up the hill and I pedaled myself up the hill.
There was no loss of momentum and I could manage a half decent cadence.

Remember, I've got an ebike that weighs almost 100 pounds with street tires, no rear suspension, 75 mm travel front forks, two mirrors, and a windshield.

Anything is possible.
You just have to try.

And have a good power to weight ratio ...

 

[dodgeman]

Interesting set of graphs. I had a lot of physics in college and knew wind resistance is usually the biggest factor. You want a tail wind going up a hill but it’s better to have the headwind going up a hill because you’re probably going slower and then get the tailwind going back down where it helps more.

 

[Art Deco]

Interesting set of graphs. I had a lot of physics in college and knew wind resistance is usually the biggest factor. You want a tail wind going up a hill but it’s better to have the headwind going up a hill because you’re probably going slower and then get the tailwind going back down where it helps more.

Very much influenced by location. I get a strong wind from the northwest reliably at sunset, but morning wind is more of a crapshoot unless it's raining ... then it's from the northwest again.